INEQUAÇAO

Para resolver o problema proposto no início da seção anterior é preciso resolver a inequação 57,55 | h - 15,64 | < 10. O exemplo abaixo mostra como resolver este tipo de desigualdade analiticamente e, também, como é possível usar gráficos para visualizar suas soluções.

Exemplo 1

Resolva | 3 x - 4 | < 5.

Solução Algébrica

Para resolver a inequação dada, você deve observar que a desigualdade | 3 x - 4 | < 5 é equivalente a - 5 < 3 x - 4 < 5.

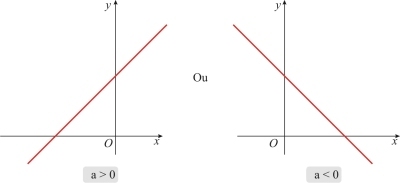
Esta equivalência se torna evidente, quando interpretamos o valor absoluto de um número como a distância deste número à origem. Dessa maneira, temos que a distância de um número x à origem é menor do que a se e somente se xestá entre a e - a , isto é  Û - a < x < a Veja a figura ao lado.

Assim, temos que

- 5 < 3 x - 4 < 5 Û - 1 < 3 x < 9 Û  < 3.

Portanto, a solução da inequação é o intervalo aberto (  ), isto é, todos os valores de x entre  e 3 satisfazem a desigualdade dada.

Solução Gráfica

Para resolver a inequação | 3 x - 4 | < 5 graficamente, começamos traçando o gráfico da função y = | 3 x - 4 | - 5. Este gráfico é mostrado ao lado.

Resolver uma desigualdade, f(x) < 0, equivale a encontrar todos os valores de x para os quais o gráfico da função está abaixo do eixox. Para achar estes valores imagine-se caminhando na direção positiva, sobre o eixo x. Enquanto caminha, vá olhando para baixo (f(x) < 0, quando o seu gráfico está abaixo do eixo x). No nosso exemplo, você verá o gráfico a partir do ponto x = - 1/3, onde o mesmo corta o eixo x, e permanecerá visível para qualquer posição que você se encontre entre os pontos x = - 1/3 e x = 3. Assim, a desigualdade será verdadeira para valores de x entre - 1/3 e 3.

Repare que para resolver uma inequação f(x) < 0, graficamente, é preciso antes de mais nada, encontrar os pontos onde o gráfico da função f intercepta o eixo x. Isto corresponde a encontrar as raízes da equação f(x) = 0. Logo, para resolver uma inequação graficamente você deve primeiro, resolver a equação corrrespondente.

TAXA DE VARIAÇAO DA FUNÇAO AFIM

O parâmetro a de uma função afim f(x) = ax + b é chamado de taxa de variação (ou taxa de crescimento). Para obtê-lo bastam dois pontos quaisquer, porem distintos (g, f(g)) e (h, f(h)), da função considerada.

Assim, f(g) = ag +b e f(h) = ah + b, onde obtemos que f(h) – f(g) = a(h – g) e, portanto:

A taxa de variação a é sempre é sempre constante para cada função afim, e isso é uma característica importante das funções afins. Por exemplo, a taxa de variação da função afim f(x) = 5x + 2 é 5 e a da função g(x) = -2x + 3 é – 2.

Observação: a taxa de variação de uma função afim f(x) = ax + b pode ser obtida fazendo f(1) – f(0). Note que f(1) = a + b e f(0) = b. Logo, f(1) – f(0) = (a + b) – b = a. Assim, f(1) – f(0) = a.

APLICAÇOES DE FUNÇAO AFIM

Exemplo 1 

Uma pessoa vai escolher um plano de saúde entre duas opções: A e B.
Condições dos planos:
Plano A: cobra um valor fixo mensal de R$ 140,00 e R$ 20,00 por consulta num certo período.
Plano B: cobra um valor fixo mensal de R$ 110,00 e R$ 25,00 por consulta num certo período.

Temos que o gasto total de cada plano é dado em função do número de consultas x dentro do período pré – estabelecido.
Vamos determinar:
a) A função correspondente a cada plano.
b) Em qual situação o plano A é mais econômico; o plano B é mais econômico; os dois se equivalem.

a) Plano A: f(x) = 20x + 140
Plano B: g(x) = 25x + 110

b) Para que o plano A seja mais econômico:
g(x) > f(x)
25x + 110 > 20x + 140
25x – 20x > 140 – 110
5x > 30
x > 30/5
x > 6

Para que o Plano B seja mais econômico:
g(x) < f(x)
25x + 110 < 20x + 140
25x – 20x < 140 – 110
5x < 30
x < 30/5
x < 6

Para que eles sejam equivalentes:
g(x) = f(x)
25x + 110 = 20x + 140
25x – 20x = 140 – 110
5x = 30
x = 30/5
x = 6

O plano mais econômico será:
Plano A = quando o número de consultas for maior que 6.
Plano B = quando número de consultas for menor que 6.

Os dois planos serão equivalentes quando o número de consultas for igual a 6.

Exemplo 2

Na produção de peças, uma fábrica tem um custo fixo de R$ 16,00 mais um custo variável de R$ 1,50 por unidade produzida. Sendo x o número de peças unitárias produzidas, determine:

a) A lei da função que fornece o custo da produção de x peças;
b) Calcule o custo de produção de 400 peças.

Respostas

a) f(x) = 1,5x + 16

b) f(x) = 1,5x + 16
f(400) = 1,5*400 + 16
f(400) = 600 + 16
f(400) = 616

O custo para produzir 400 peças será de R$ 616,00.

Exemplo 3

Um motorista de táxi cobra R$ 4,50 de bandeirada mais R$ 0,90 por quilômetro rodado. Sabendo que o preço a pagar é dado em função do número de quilômetros rodados, calcule o preço a ser pago por uma corrida em que se percorreu 22 quilômetros?

f(x) = 0,9x + 4,5
f(22) = 0,9*22 + 4,5
f(22) = 19,8 + 4,5
f(22) = 24,3

O preço a pagar por uma corrida que percorreu 22 quilômetros é de R$ 24,30

FUNÇAO AFIM

                                         



CONCEITO:Uma função definida por f: R→R chama-se afim quando existem constantes a, b que pertencem ao conjunto dos reais tais que f(x)= ax + b para todo x ∈ R. A lei que define função afim é:

O gráfico de uma função afim é uma reta não perpendicular ao eixo Ox.